いよいよ入試まであと2か月となってきました。今年の都立入試ではどんな問題が出題されるのか、今から楽しみです。都立高校入試では4⃣に平面図形が出題され、その中には相似を使った面積比の問題も良く出題されます。2種類以上の相似な図形が見つかった場合は連比を使って線分の比を求めると、簡単に面積比がわかります。そこで今回は連比の使い方と連比を使って面積比を解く方法をお教えします。

問題

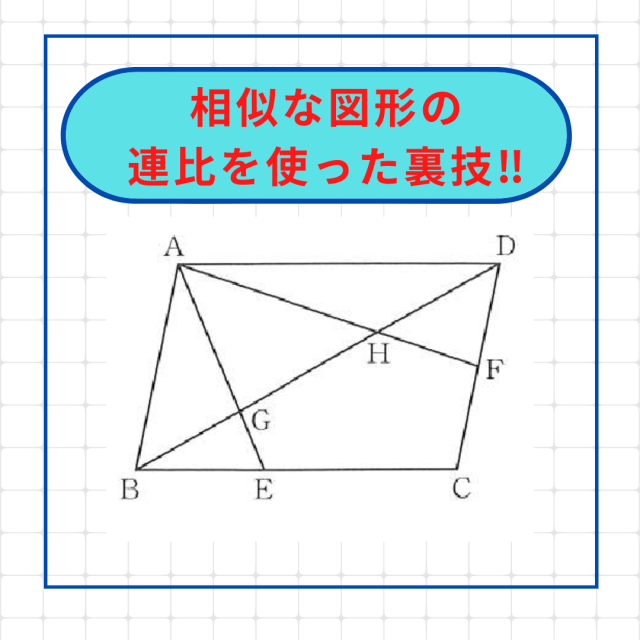
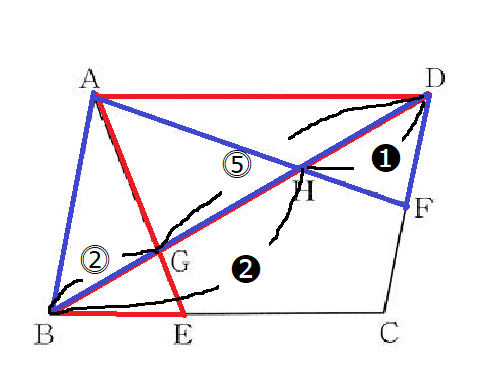
右の図の▱ABCDでEはBCを2：3に分ける点，FはDCの中点である。線分AE，AFが対角線BDと交わる点をそれぞれG，Hとする。このとき，△AGHの面積は▱ABCDの面積の何倍か。

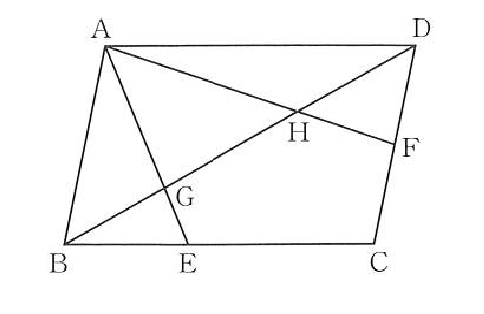
①図形の中に相似を見つけましょう。2種類あります。

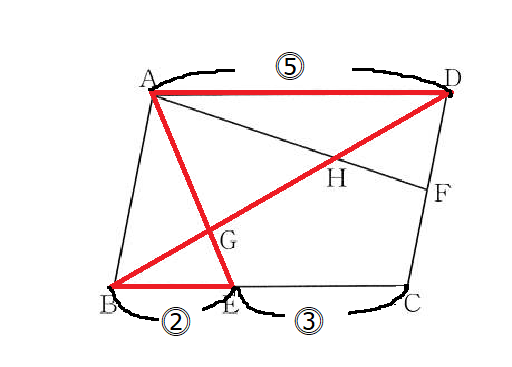
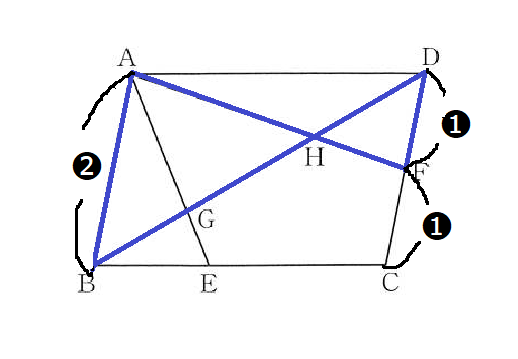
BE：EC＝⓶：⓷より平行四辺形の向かい側の辺ADは⓹とわかり平行線の錯角が等しいので2組の角がそれぞれ等しいので、△AGD∽△EGB＝⓹：⓶の相似とわかります。 また、ＦはＤＣの中点なのでＤＦ：ＦＣ＝❶：❶より平行四辺形の向かい側の辺ＡＢは❷とわかります。同様に△ＡＢＨ∽△ＦＤＨ＝❷：❶の相似とわかります。

②次に連比を求めていきます。

連比とは3つ以上の比の表し方のことです。いつ連比を使えばよいのか、というところですが図のように一本の線分上に交点が２つあるときには2種類の相似を見つけて連比(ＢＧ：ＧＨ：ＨＤ)を作るようにしましょう。

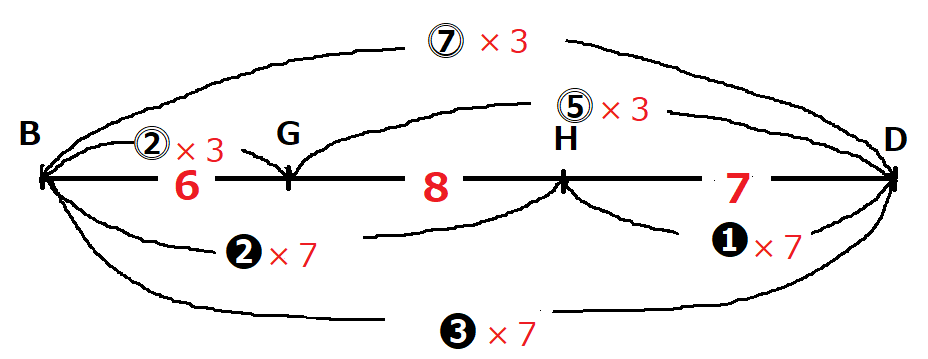
2つの相似比をＢＤ上に書きこんでみるとＢＧ：ＧＤ＝⓶：⓹，ＢＨ：ＨＤ＝❷：❶となります。まず全体の比は⓻と❸なので7と3の最小公倍数である㉑にそろえます。よってBG：GD＝⓶×３：⓹×３＝６：15，BH：HD＝❷×７：❶×７＝14：７となり、ＢＧ：ＧＨ：ＨＤ＝６：８：７とわかります。 図の中でやるとわからない場合は、線分BDだけ取り出して書き出してみるとわかりやすいです。

③面積比を求めよう。

面積比の基本事項として、高さが等しい三角形の場合は底辺比がそのまま面積比になります。

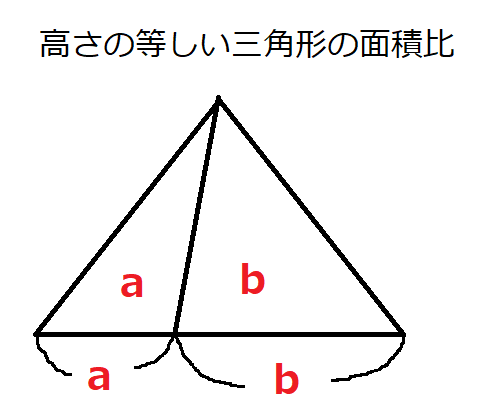
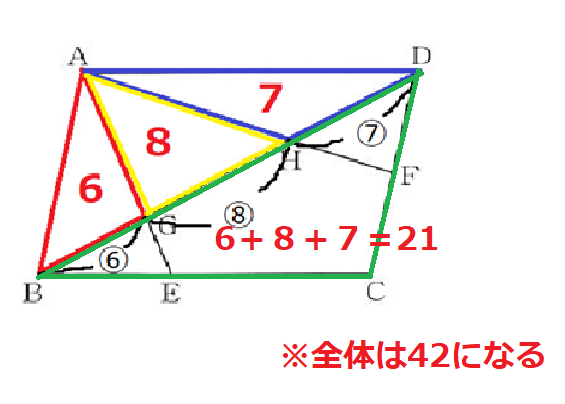
したがって、先ほど求めたＢＧ：ＧＨ：ＨＤ＝６：８：７より、面積比もそのまま△ＡＢＧ：△ＡＧＨ：△ＡＨＤ＝６：８：７となります。

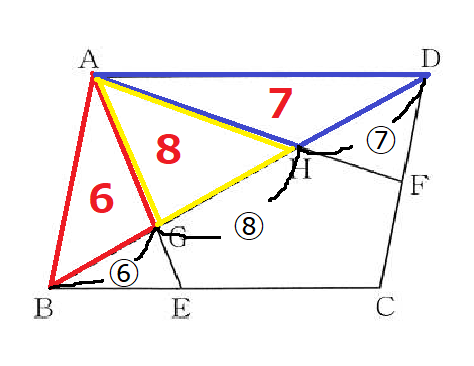
④ここからが重要！

平行四辺形の対角線は面積を半分にしていることに注目しましょう。したがって、△ＡＢＤ＝△ＢＣＤとなり、△ＡＢＤの面積比は６＋８＋７＝21になるので△ＢＣＤの面積比も21となり、▱ＡＢＣＤの面積は21＋21＝42となります。

△ＡGＨの面積比は８なので、△ＡGＨの面積は▱ＡＢＣＤの面積の8÷42＝4/21倍が正解です。

ベスト自修館の冬期講習

ベスト自修館は入試までの最終版、最後まで役立つ授業をスタッフ全員で受験生のみなさんに提供していきます。そのほかの学年のみなさんにもご要望にあわせたさまざまな冬期講習、その他特別講座をご用意しております。ベスト自修館の冬期講習を受講して、今年１年の締めくくりと来年の良いスタートを切れるよう頑張ってみませんか。