いよいよ入試が近づいてきました。毎年都立高校入試では5⃣番問題に立体図形が出題されます。問１には立体の中にできる角度や三平方の定理を使った長さ、中点連結定理を使った問題などが出題され、問２では体積を求める問題が出題されます。今回は体積比を使って解く裏技をお教えします。受験生の皆さん、最後の最後まで全力で頑張って合格を勝ち獲ってください。

（問題）

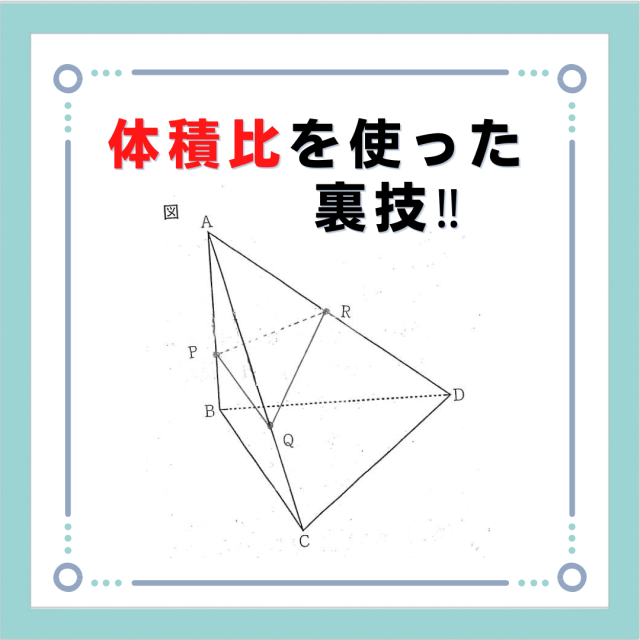
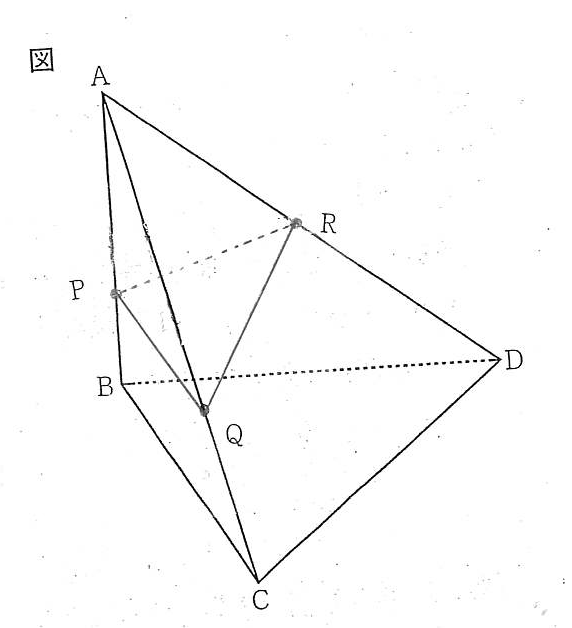
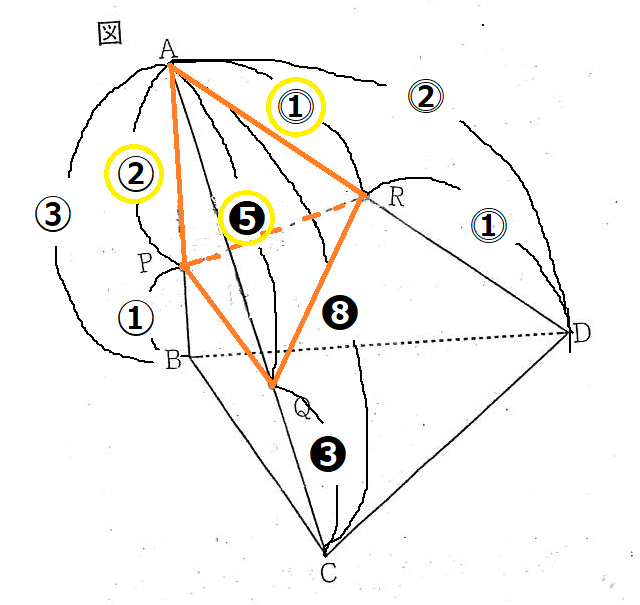
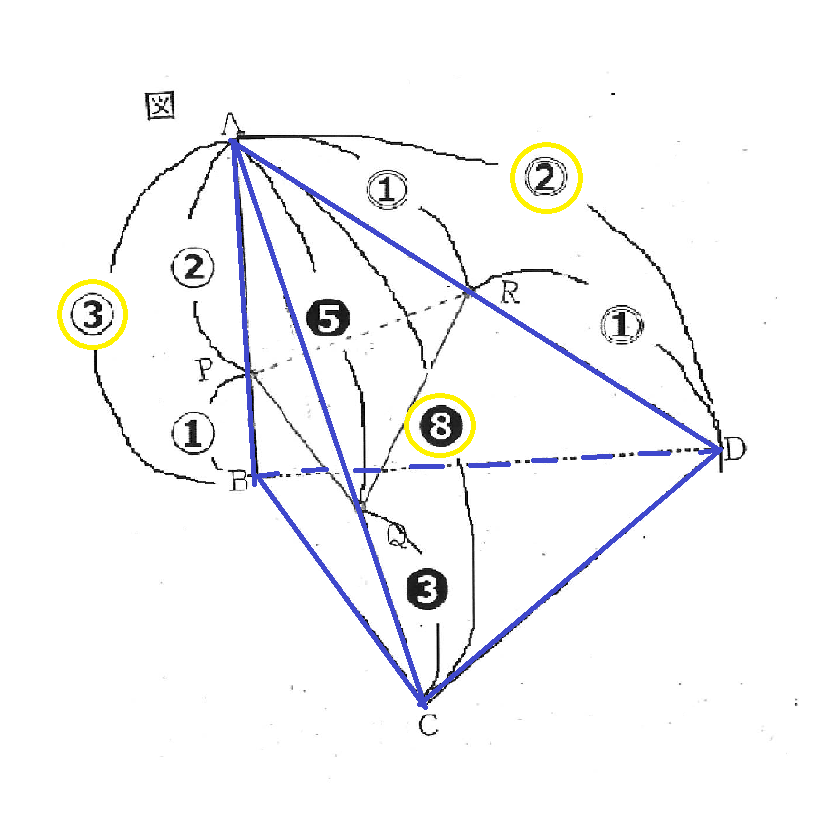
右の図に示した立体A－BCDは，AB＝BC＝6㎝，BD＝8㎝，CD＝10㎝，∠ABC＝∠ABD＝∠CBD＝90°の三角錐である。 辺AB上にあり，AP：PB＝2：1になる点をP，辺AC上にあり，AQ：QC＝5：3になる点をQ，辺ADの中点をRとするとき，立体A－PQRの体積を求めなさい。

(解き方)

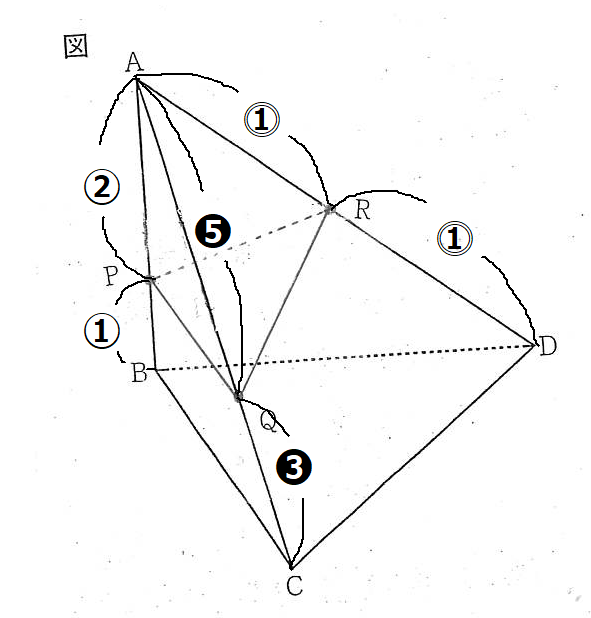
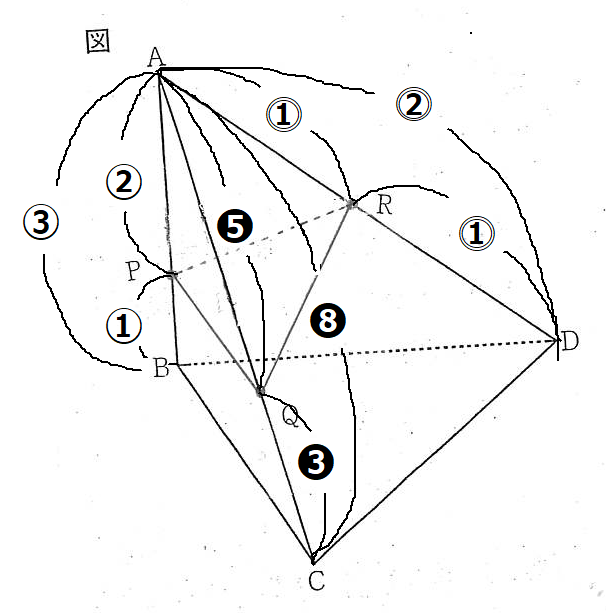
AP：PB＝2：1より，AP：AB＝②：③となります。また、AQ：QC＝5：3より，ＡＱ：ＡＣ＝❺：❽となります。また，点Ｒは辺ＡＤの中点なので，ＡＲ：ＲＤ＝1：1より，ＡＲ：ＡＤ＝⓵：⓶となります。

（立体Ａ－ＰＱＲの体積と立体Ａ－ＢＣＤの体積比を求めよう。）

ここで裏技を覚えておこう！三角錐の体積比の求め方は、頂点から出ている3辺の比をかけた比が体積比となります。 したがって、立体Ａ－ＰＱＲ：立体Ａ－ＢＣＤ＝(②×❺×⓵)：(③×❽×⓶)=10：48＝５：24となります。

立体Ａ－ＢＣＤの体積は8×8×1/2×６×1/3＝64より，5：24＝ⅹ：64，ⅹ＝40/3(㎤) よって、立体A－PQRの体積は40/3(㎤)となります。

今年度の都立入試では5⃣に三角錐の体積が出題されるかもしれません。この裏技を覚えておけば、今からでも数学の当日点がプラス５点UPできるかもしれませんので、ぜひ活用してみてくださいね。ちなみに、数学で最も重要なことは、出来る問題でミスをしないことですよ。

(ベスト自修館の新年度授業)

なお、ベスト自修館は３月２日(木)より全ての学年が新学年となり、新年度授業がスタートします。４月から塾をお考えの方も、塾は３月から先取りの授業を行っていますので、お早めにお問い合わせください。無料体験授業などもございますので、お気軽にお問合せ下さい。ベスト自修館は受験生に限らず、生徒の皆さんに役立つ授業をスタッフ全員で提供していきます。